Il mistero della scacchiera mutilata – I grandi rompicapo – Emma la pasticciera, nota cultrice dei rompicapo matematici e dei problemi di logica (Pagina Ufficiale di Emma) dopo un lungo studio ha deciso di selezionare i giochi logico-matematico più belli di ogni tempo proponendone separatamente anche le relative soluzioni.
Si tratta di quesiti che per essere risolti richiedono doti sia logiche ma anche creative. Il rompicapo matematico perfetto deve proporre una situazione semplice da spiegare e una soluzione altrettanto immediata da comprendere ma complicatissima da trovare, spesso al limite dell’impossibile per una mente media.
In questa pagina presentiamo Il mistero della scacchiera mutilata, un altro gioco di logica (dopo Il problema dei tre interruttori) dove è necessario attivare il c.d. pensiero laterale… Con il termine pensiero laterale, coniato dallo psicologo maltese Edward de Bono, si intende una modalità di risoluzione di problemi logici che prevede un approccio particolare, ovvero l’osservazione del problema da diverse angolazioni, contrapposta alla tradizionale modalità che prevede concentrazione su una soluzione diretta al problema.
Una soluzione diretta prevede il ricorso alla logica sequenziale, risolvendo il problema partendo dalle considerazioni che sembrano più ovvie, il pensiero laterale se ne discosta (da cui il termine laterale) e cerca punti di vista alternativi per cercare la soluzione.
IL MISTERO DELLA SCACCHIERA MUTILATA
Emma ricorda spesso la prima lezione di matematica all’Università dove il professore, appena entrato nel auditorium zeppo di matricole del primo anno si presentò disegnando sulla lavagna un reticolato a forma di scacchiera 8×8 e poi due quadrai congiunti.
“Questa è una scacchiera 8×8 di 64 caselle. Questo è un pezzo del domino che le cui dimensioni sono esattamente quelle di due caselle della scacchiera contigue”.
“Con 32 pezzi del domino quindi si può coprire perfettamente la scacchiera con 8 colonne formate da 4 pezzi del domino posizionati in verticale.”
“Fino a qui non c’è bisogno di un genio!” ridacchiò il professore pulendosi al vestito le mani sporche di gesso.
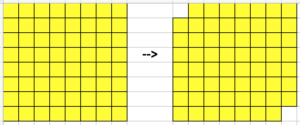
“Il problema è che un mio amico a quella scacchiera ha segato due angoli opposti – esclamò il professore – quindi la scacchiera mutilata è composta da 62 caselle”.
La domanda quindi è semplice:
E’ possibile coprire perfettamente tale scacchiera ridotta con 31 pezzi del domino interi, cioè senza spezzarli?
(La Soluzione è in fondo pagina)
INTERMEZZO MUSICALE
Flying the Dolomites
L’altalena della memoria
Colori sonori
SOLUZIONE
Vieni a scoprire il magico mondo musicale di Lorenzo Pescini!
Pescini.com – Tutti i diritti riservati – ART336